파이썬 / BOJ 백준 / 1149번 RGB 거리 - dp
https://www.acmicpc.net/problem/1149
1149번: RGB거리
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나
www.acmicpc.net
문제
RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.
집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.
1번 집의 색은 2번 집의 색과 같지 않아야 한다.
N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.
풀이
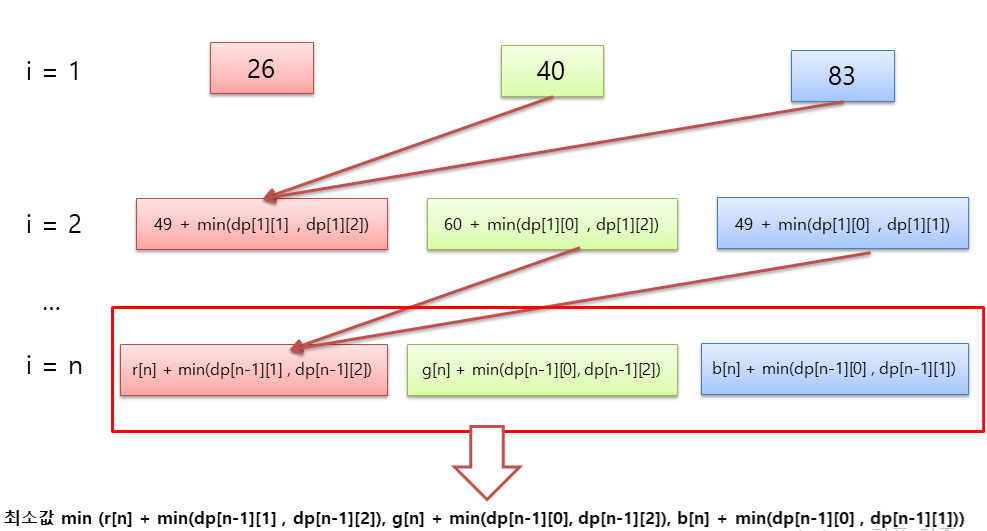
1. dp는 각 색상에 대하여 누적 최소값을 나타냅니다.
2. 첫번째의 dp[0][0], dp[0][1], dp[0][2]의 값은 각각 빨간색, 초록색, 파란색의 첫번째 값을 넣어줍니다.
3. 2번째 값부터는 집이 연속된 색상을 가지지 말아야 합니다. 그래서 빨간색 집의 dp는 현재 빨간색의 집 칠하는 비용과 이전의 초록색 집의 dp와 파란색 집의 dp 중 작은 값을 넣어 줍니다.
그러면 red[n] + min(dp[n-1][1] , dp[n-1][2]) 와 같은 식이 만들어 집니다.
4. 초록색 집의 dp와 파란색 집의 dp도 이와 유사하게 구합니다.
5. 이렇게 구해진 값 dp[n][0], dp[n][1], dp[n][2] 중 최소값을 선택하면 됩니다.
전체 코드
n = int(input())
dp = []
for i in range(n):
dp.append(list(map(int, input().split())))
for i in range(1, len(dp)):
#print(dp[i][0], dp[i][1], dp[i][2])
dp[i][0] = min(dp[i - 1][1], dp[i - 1][2]) + dp[i][0]
dp[i][1] = min(dp[i - 1][0], dp[i - 1][2]) + dp[i][1]
dp[i][2] = min(dp[i - 1][0], dp[i - 1][1]) + dp[i][2]
#print("sum : ", dp[i][0], dp[i][1], dp[i][2])
print(min(dp[n - 1][0], dp[n - 1][1], dp[n - 1][2]))'BOJ 백준 알고리즘 > 동적 프로그래밍 DP' 카테고리의 다른 글
| 파이썬 / BOJ 백준 / 2579번 계단 오르기 - dp (0) | 2021.08.19 |
|---|---|
| 파이썬 / BOJ 백준 / 1932번 정수 삼각형 - dp (0) | 2021.08.18 |
| 파이썬 / BOJ 백준 / 9461번 파도반 수열 - dp (0) | 2021.08.16 |
| 파이썬 / BOJ 백준 / 1904번 01타일 - dp (0) | 2021.08.15 |
| 파이썬 / BOJ 백준 / 9184번 신나는 함수 실행 - dp (0) | 2021.08.15 |