해커를 꿈꾸는 개발자

파이썬 / BOJ 백준 / 12865 평범한 배낭 - dp

https://www.acmicpc.net/problem/12865

문제

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다.

준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

풀이

1. 유명한 냅색 문제입니다.

2. 배낭의 용량이 정해져 있을 때, 최대한의 가치를 가지도록 배낭을 싸야 하고, 주어진 물건들의 용량과 가치를 고려하여 주워담을지 말지 정하는 문제입니다.

3. DP 2차 배열을 만들어, DP[아이템 번호][무게]로 놓고, 그 무게에 최대한의 아이템을 넣었을 경우의 최대 가치를 값으로 넣습니다.

=> dp [i - 1][j]: i번째 아이템을 챙기지 않았을 때의 최댓값

=> dp [i - 1][j - weight [i]] + value [i]]: i번째 아이템을 챙겼을 때 갖는 최댓값

4. j의 무게가 현재 아이템의 무게보다 크거나 같다면 아래와 같은 식을 세웁니다.

dp [i][j] = max(dp[i - 1][j], dp[i - 1][j - weight [i]] + value [i]]

5. j의 무게가 현재 아이템의 무게보다 작다면 아래와 같은 식을 세웁니다.

dp[i][j] = dp[i - 1][j]

6. 마지막으로 DP[N][K]의 값이 문제에서 원하는 답이 됩니다.

예시의 입력값에 대하여 문제를 풀어 보도록 하겠습니다. 

j가 6일 때, dp[0][6]과 dp[0][0] + 13과 비교하여, 큰 값인 13이 입력됩니다.

j가 7일 때도, dp[0][7]과 dp[0][1] + 13과 비교하여, 큰 값인 13이 입력됩니다.

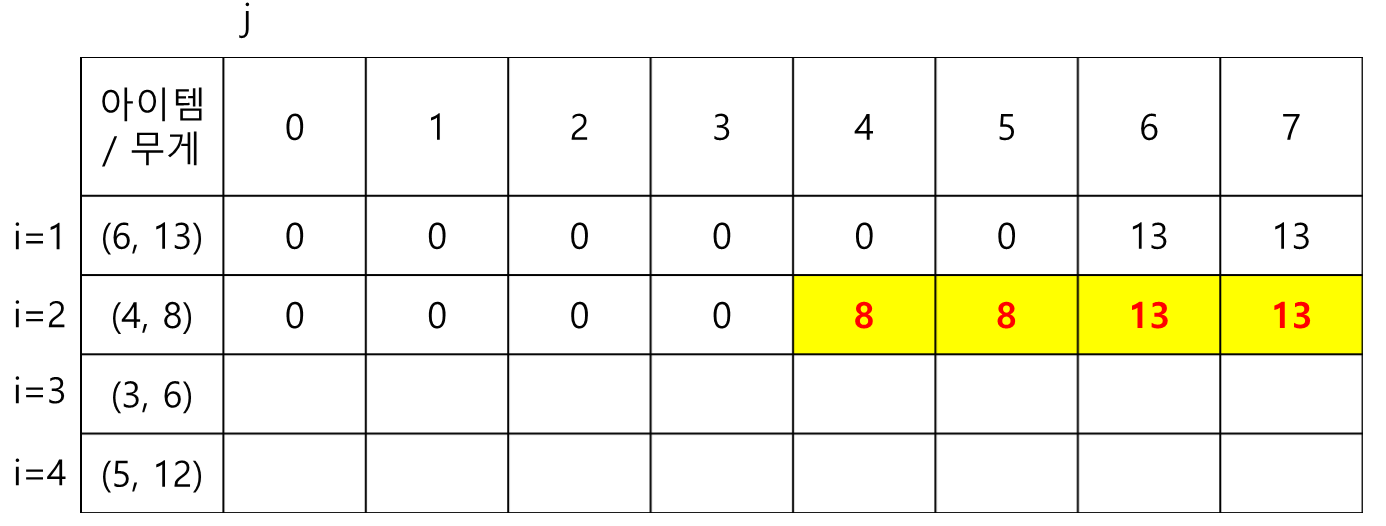
j가 4일 때, dp[1][4]과 dp[1][0] + 8과 비교하여, 큰 값인 8이 입력됩니다.

j가 5일 때도, dp[1][5]과 dp[1][1] + 8과 비교하여, 큰 값인 8이 입력됩니다.

j가 6일 때는, dp[1][6]과 dp[1][2] + 8과 비교하여, 큰 값인 13이 입력됩니다.

j가 3일 때, dp[2][3](=0)과 dp[2][0] + 6과 비교하여, 큰 값인 6이 입력됩니다.

j가 4일 때는, dp[2][4](=8)과 dp[2][1] + 6과 비교하여, 큰 값인 8이 입력됩니다.

j가 6일 때는, dp[2][6](=13)과 dp[2][3] + 6과 비교하여, 큰 값인 13이 입력됩니다.

j가 7일 때는, dp[2][6](=13)과7dp[2][4](=8) + 6과 비교하여, 큰 값인 14이 입력됩니다.

위와 동일한 방식으로 비교하였을 경우, 위 테이블과 같이 입력됩니다.

따라서, 답은 DP[N][K]의 값인 14가 됩니다.

전체 코드

import sys

n, k = map(int, sys.stdin.readline().split())
dp = [[0] * (k + 1) for _ in range(n + 1)]

for i in range(1, n + 1):
    w, v = map(int, input().split())
    for j in range(1, k + 1):
        if w > j:
            dp[i][j] = dp[i - 1][j]
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w] + v)
print(dp[n][k])

파이썬 / BOJ 백준 / 1912 연속합 - dp

https://www.acmicpc.net/problem/1912

문제

n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.
예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.

풀이

1. DP 문제입니다.

2. DP의 i-1번째의 값이 0보다 크면, DP[i] = DP[i-1] + Arrar[i] 해줍니다.

3. DP의 i-1번째의 값이 0보다 작으면, DP[i]에는 배열의 i의 값을 넣어줍니다.

=> DP[i] = Arrar[i]

4. DP 리스트의 값중 가중 큰 값을 출력합니다.

전체 코드

n = int(input())
a = list(map(int, input().split()))

INF = -float("inf")
dp = [INF] * 100002
dp[0] = a[0]

for i in range(1, n):
    if dp[i-1] > 0:
        dp[i] = dp[i-1] + a[i]
    else:
        dp[i] = a[i]

print(max(dp))

파이썬 / BOJ 백준 / 9251 LCS - dp

https://www.acmicpc.net/problem/9251

문제

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.
예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

풀이

1. LCS(Longest Common Subsequence, 최장 공통 부분 수열)는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 부분을 말합니다.

2. ACAYKP를 비교 대상으로 잡고 CAPCAK 문자열 하나씩 추가하면서 공통 수열 길이 값을 DP 테이블에 표시해줍니다.

3. 문자열이 같으면 왼쪽 대각선 위의 값에 +1을 합니다.

4. 문자열이 같지 않으면, 왼쪽의 값과 위쪽의 값 중 큰 값을 넣습니다.

5. DP의 마지막 값인 DP[-1][-1]의 값이 최장 공통 부분 수열의 길이가 됩니다.

6. 위의 DP 테이블을 보면 노란색으로 칠한 부분이 최장 공통 부분 수열로 ACAK이고, 길이는 4가 됩니다.

전체 코드

m = ' ' + input()
n = ' ' + input()

dp = [[0] * (len(n)) for i in range(len(m))]

for i in range(1, len(m)):
    for j in range(1, len(n)):
        if m[i] == n[j]:
            dp[i][j] = dp[i-1][j-1] + 1
        else:
            dp[i][j] = max(dp[i-1][j], dp[i][j-1])
print(dp[-1][-1])

파이썬 / BOJ 백준 / 2565 전깃줄 - dp

https://www.acmicpc.net/problem/2565

문제

두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.

전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.

풀이

1. dp로 풀 수 있는 문제입니다.

2. a 전봇대 기준으로 정렬하고, b전봇대 기준으로 가장 긴 증가하는 부분수열의 길이를 구해주면 연결될 수 있는 최대 전깃줄이 나옵니다.

가장 긴 증가하는 부분수열은 https://zidarn87.tistory.com/285 링크를 참고하시면 됩니다.

3. 답은 N – 최대 전깃줄의 수로 출력하면 됩니다.

4. 위 표와 같이 8개의 전깃줄 중에 가장 긴 증가하는 부분수열의 길이는 5가 나오는데, 총 전깃줄의 수 8개 – 5개 하면, 없애야 하는 전깃줄은 3개가 나옵니다.

전체코드

import sys

n = int(sys.stdin.readline().strip())
elec_list = []
for i in range(n):
    x, y = map(int, sys.stdin.readline().split())
    elec_list.append((x,y))

elec_list.sort()
dp = [1 for _ in range(n)]
#print(elec_list)

for i in range(n):
    for j in range(i):
        if elec_list[i][1] > elec_list[j][1]:
            dp[i] = max(dp[i], dp[j] + 1)

print(n - max(dp))